四元数（Quaternion）

    最近在做的工作是深度点云, 在学习计算机图形学和刚体运动的过程中接触到四元数, 本身是一个比较抽象的概念, 我们都知道复数可以画成一个2维平面, 复数的乘法表示2维的拉伸和旋转, 那么四元数呢? 下面会一步步来学习四元数是如何表示三维旋转的.

>>

1. 复数（Complex Number）

1.1 定义

    在介绍四元数之前, 先来了解复数和2D旋转之间的关系, 由于不是本文重点所以就简单介绍一下.
    任意一个复数$\mathcal z \in \mathbb C$都可以表示成 $\mathcal z =\mathcal a +\mathcal b \mathcal i$ 的形式, 其中$\mathcal a \mathcal b \in \mathbb R$而且$i^2=-1$. 其中$\mathcal a$和$\mathcal b$就是这个复数的实部(Real Part)和虚部(Imagirary Part).
表示为向量形式就是:

$$\mathcal z = \left[ \begin{matrix} \mathcal a\\ \mathcal b \end{matrix} \right]$$

     如此一来, 在复平面上也就形成一条直线.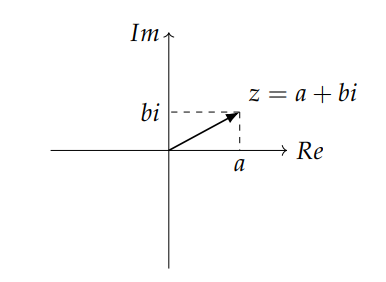

1.2 复数乘法

    考虑两个复数$\mathcal z_1 = \mathcal a + \mathcal b \mathcal i$和$\mathcal z_2 = \mathcal c +\mathcal d \mathcal i$, 利用分配律直接相乘:

$$\mathcal z_1 \mathcal z_2 = (\mathcal a + \mathcal b \mathcal i)(\mathcal c + \mathcal d \mathcal i)\\ =\mathcal a \mathcal c + \mathcal a \mathcal d \mathcal i + \mathcal b \mathcal c \mathcal i + \mathcal b \mathcal d \mathcal i^2\\ = \mathcal a \mathcal c - \mathcal b \mathcal d + \mathcal a \mathcal d \mathcal i + \mathcal b \mathcal c \mathcal i\\ = \mathcal a \mathcal c - \mathcal b \mathcal d + (\mathcal b \mathcal c + \mathcal a \mathcal d)\mathcal i$$

    可以发现, 复数相乘其实就是矩阵相乘:

$$\mathcal a \mathcal c - \mathcal b \mathcal d + (\mathcal b \mathcal c + \mathcal a \mathcal d)\mathcal i \\= \left[ \begin{matrix} \mathcal a & \mathcal -b\\ \mathcal b & \mathcal a \end{matrix} \right] \left[ \begin{matrix} \mathcal c\\ \mathcal d \end{matrix} \right]$$

    需要注意的是, 尽管形式上等价于矩阵相乘, 但是交换$\mathcal z_1 \mathcal z_2$的位置会得到相同的计算结果, 这里就不写了.

1.2 复数模长（Magnitude）与共轭（Conjugate）

    还是$\mathcal z = \mathcal a + \mathcal b \mathcal i$, 它的模长也就表示为

$$\Vert z \Vert = \sqrt{a^2+b^2}$$

     它的共轭表示为

$$\bar z = a-bi$$

    我们发现只需要翻转虚部就可以得到共轭, 并且模长可以通过共轭乘积得到

$$\Vert z \Vert = \sqrt{z\bar z}$$

    大家可以自己算一下$z\bar z$, 简单的分配律即可, 这里就不算了.

1.3 复数与2D旋转

    前面说过复数相乘可以表示为$\left[ \begin{matrix} a & -b \ b & a \end{matrix} \right]$矩阵做出变换, 对该矩阵变形:

$$\left[ \begin{matrix} a & -b \\ b & a \end{matrix} \right] = \sqrt{a^2 + b^2} \left[ \begin{matrix} \frac{a}{\sqrt{a^2+b^2}} & \frac{-b}{\sqrt{a^2+b^2}} \\ \frac{b}{\sqrt{a^2+b^2}} & \frac{a}{\sqrt{a^2+b^2}} \end{matrix} \right]$$

    每个元素除以模长, 观察复平面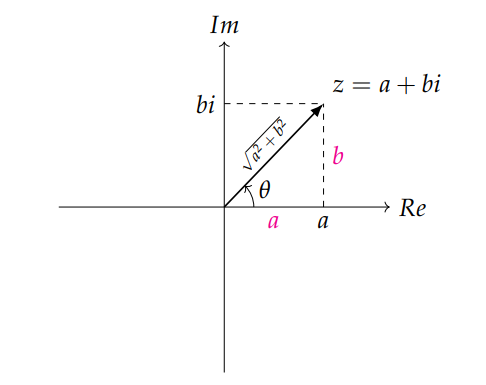

    会发现$\Vert z \Vert$正是复数$z$与坐标轴所形成三角形的斜边长, 而$a, b$正是三角形的两条边, 记录夹角为$\theta$, 那么可以得到$\cos({\theta}) = \frac{a}{\sqrt{a^2+b^2}}$并且$\sin({\theta})=\frac{b}{\sqrt{a^2+b^2}}$, OK, 那么接下来继续对矩阵变形.

$$\left[ \begin{matrix} a & -b \\ b & a \end{matrix} \right]=\sqrt{a^2 + b^2}\left[ \begin{matrix} \frac{a}{\sqrt{a^2+b^2}} & \frac{-b}{\sqrt{a^2+b^2}} \\ \frac{b}{\sqrt{a^2+b^2}} & \frac{a}{\sqrt{a^2+b^2}} \end{matrix} \right]\\ =\Vert z \Vert \left[ \begin{matrix} \cos({\theta}) & -\sin({\theta})\\ \sin({\theta}) & \cos({\theta}) \end{matrix} \right]\\ =\Vert z \Vert I \left[ \begin{matrix} \cos({\theta}) & -\sin({\theta})\\ \sin({\theta}) & \cos({\theta}) \end{matrix} \right]\\ =\left[ \begin{matrix} \Vert z \Vert & 0\\ 0 & \Vert z \Vert \end{matrix} \right]\left[ \begin{matrix} \cos({\theta}) & -\sin({\theta})\\ \sin({\theta}) & \cos({\theta}) \end{matrix} \right]$$

    变形完之后, 左边就是缩放矩阵, 右边就是我们常说的旋转矩阵了. 关于旋转矩阵的内容就不多写了.

2. 三维空间中的旋转

    先来简单说说三维空间的旋转, 三维空间的旋转有很多表示方法, 其中欧拉角是比较常见并且很好理解的方式, 也有许多问题, 比如Gimbal Lock, 并且依赖三个坐标轴的选定, 有兴趣可以找些相关资料看, 这里说一下轴角式(Axis-angle).
    假设我们有一个经过原点的(如果旋转轴不经过原点我们可以先将旋转轴平移到原点, 进行旋转, 再平移回原处)旋转轴$\mathbf u=(x,y,z)^T$, 有一个向量$\mathbf v$, 沿着这个旋转轴旋转$\theta$度, 变换到$\mathbf v^′$: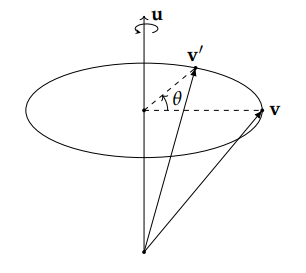

    遵循右手定则, 右手拇指指向$\mathbf u$正向, 弯曲的手指为旋转正向.
    在轴角式中, 旋转的定义需要四个变量: $x,y,z,\theta$, 换句话说, 我们具有四个自由度(Degree of Freedom), 而欧拉角只有三个自由度, 然而实际上三个自由度确实能够得到一个旋转, 那么为什么这里多出一个自由度?
    事实上, 在定于旋转轴$x,y,z$的同时, 也就定义了$\mathbf u$的模长, 平时所说的绕着一个向量$\mathbf u$做旋转, 其实是指绕着$\mathbf u$所指的方向进行旋转. 我们知道向量具有方向和大小两个性质, 在旋转中大小并不重要, 这应该很好理解, 绕着$\mathbf u_1=(0, 0, 1)^T$和绕着$\mathbf u_2=(0, 0, 3)^T$是一样的, 虽然这两个向量的长度不同, 但它们指向通一个方向(也就为旋转指明了方向).
    在三维空间中, 定义方向只需要两个量, 举个例子, 地球的经纬度, 而如果需要某个方位上的特定一点, 还需要一个自由度, 也就是海拔.
    为了消除模长这个自由度, 规定旋转轴$\mathbf u$的模长为1, 也就是$\Vert \mathbf u \Vert=\sqrt{x^2+y^2+z^2}=1$, 这样一来只要给出$\mathbf u$的任意两个坐标, 就可以求出第三个坐标. 当然, 也可以不规定模长为1, 但是为了后续的许多推倒便利, 规定为1是有好处的, 这也是数学和物理中对方向定义的惯性.

2.1 旋转的分解

    在进行旋转之前, 先对旋转进行分解. 首先将$\mathbf v$分解为平行于旋转轴$\mathbf u$和正交与旋转轴$\mathbf u$的两个分量, 记做$\mathbf v_\Vert$和$\mathbf v_\bot$.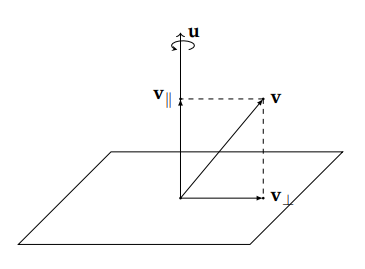

    那么就有以下等式:

$$\mathbf v=\mathbf v_\Vert + \mathbf v_\bot \tag{1}$$

    分别旋转两个分量, 得到$\mathbf v_\Vert^′$和$\mathbf v_\bot^′$, 同样:

$$\mathbf v=\mathbf v_\Vert^′ + \mathbf v_\bot^′ \tag{2}$$

    事实上$\mathbf v_\Vert$就是就是$\mathbf v$在$\mathbf u$上的正交投影 (Orthogonal Projection):

$$\mathbf v_\Vert=proj_\mathbf u (\mathbf v)\\ =\frac {\mathbf u· \mathbf v}{\mathbf u · \mathbf u} \mathbf u\\ =\frac {\mathbf u· \mathbf v}{\Vert \mathbf u \Vert^2} \mathbf u\\ =(\mathbf u · \mathbf v) \mathbf u\\$$

    由于(1), 可以得到$\mathbf v_\bot = \mathbf v - \mathbf v_\Vert = \mathbf u - (\mathbf u · \mathbf v) \mathbf u$, 至此就能知道如何根据得到的$\mathbf u, \mathbf v$得到分量了, 要旋转$\mathbf u, \mathbf v$, 需要对分量进行旋转.

2.2 $\mathbf v_\Vert$的旋转

    从图里可以知道, $\mathbf v_\Vert$根本没有被旋转, 因此旋转$\theta$度后有$\mathbf v_\Vert = \mathbf v_\Vert^′$.

2.3 $\mathbf v_\bot$的旋转

    $\mathbf v_\bot$与$\mathbf u$正交, 旋转可以看作是平面内的一次旋转, 现在3D旋转被转换为2D旋转, 在这个平面上我们只有一个向量$\mathbf v_\bot$, 用它来表示一个旋转是不够的, 还需要构造一个同时正交于$\mathbf u$和$\mathbf v_\bot$的向量$\mathbf w$, 通过叉乘来得到:

$$\mathbf w = \mathbf u × \mathbf v_\bot$$

    这个新的向量$\mathbf w$指向$\mathbf v_\bot$逆时针(正向)旋转$\frac {π}{2}$后的方向, 并且也处于正交平面内. 由$\Vert \mathbf u \Vert = 1$可知:

$$\Vert \mathbf w \Vert = \Vert \mathbf u × \mathbf v_\bot \Vert \\ = \Vert \mathbf u \Vert ·\Vert \mathbf v_\bot \Vert ·\sin({π/2}) \\ = \Vert \mathbf v_\bot \Vert$$

    也就是说, $\mathbf w$和$\mathbf v_\bot$的模长是相同的, 所以, $\mathbf w$也位于圆上. 有了这个新的向量, 就相当于我们在新的平面内有了两个坐标轴. 现在可以把$\mathbf v_\bot^′$投影到$\mathbf w$和$\mathbf v_\bot$上, 将其分解为$\mathbf v_v^′$和$\mathbf v_w^′$. 利用一些三角形的知识, 我们可以得到:

$$\mathbf v^′ = \mathbf v_v^′ + \mathbf v_w^′\\ =\cos({\theta}) \mathbf v_\bot + \sin({\theta}) \mathbf w\\ =\cos({\theta}) \mathbf v_\bot + \sin({\theta}) (\mathbf u × \mathbf v_\bot)$$

    因此, 旋转公式为:

$$\mathbf v_\bot^′ = cos({\theta}) \mathbf v_\bot + \sin({\theta})(\mathbf u × \mathbf v_\bot)$$

2.4 $\mathbf v$的旋转

    所以总结起来就是:

$$\mathbf v^′ = \mathbf v_\Vert^′ + \mathbf v_\bot^′\\ = \mathbf v_\bot + \cos({\theta})\mathbf v_\bot + \sin({\theta})(\mathbf u × \mathbf v_\bot)\\ = \mathbf v_\bot + \cos({\theta})\mathbf v_\bot + \sin({\theta})(\mathbf u ×(\mathbf v - \mathbf v_\Vert))\\ = \mathbf v_\bot + \cos({\theta})\mathbf v_\bot + \sin({\theta})(\mathbf u ×\mathbf v - \mathbf u × \mathbf v_\Vert)\\ \mathbf v_\bot + \cos({\theta})\mathbf v_\bot + \sin({\theta})(\mathbf u ×\mathbf v) \tag{3}$$

    将$\mathbf v_\Vert = (\mathbf u · \mathbf v) \mathbf u$和$\mathbf v_\bot=\mathbf v - (\mathbf u · \mathbf v) \mathbf u$代入(3):

$$\mathbf v^′ = (\mathbf u · \mathbf v)\mathbf u + \cos({\theta})(\mathbf v - (\mathbf u · \mathbf v) \mathbf u) + \sin({\theta})(\mathbf u × \mathbf v) \tag{4}$$

    公式(4)就表示了3D空间中任意一个$\mathbf v$沿着单位向量$\mathbf u$旋转$\theta$角度后得到的$\mathbf v^′$, 这条公式将会与四元数有所联系.

3. 四元数

    至此将会正式学习四元数, 其定义和复数非常类似, 唯一的区别在于四元数有三个虚部. 所有四元数$\mathcal q \in \mathbb H$都这样表示:

$$\mathcal q = a+bi + cj + dk (a,b,c,d \in \mathbb R)$$

    向量形式:

$$q = \left[ \begin{matrix} a\\b\\c\\d \end{matrix} \right]$$

    此外, 还可以将实部虚部分开, 用三维向量表示虚部:

$$q = [s, \mathbf v] (\mathbf v = \left[ \begin{matrix} x\\y\\z \end{matrix} \right], s,x,y,z \in \mathbb R)$$

其他内容后续再写…